Morpion Solitaire - Limites des Scores

Il est impossible d'avoir un nombre infini de coups au Morpion Solitaire. Toute partie a un nombre de coups compris entre ces limites :

On peut aussi remarquer que, par définition de leurs règles, un score record 5T ne peut PAS être meilleur que les scores records 5T+/5T#/5T++ (jeux aux règles plus libres), eux-même limités par la même borne haute :

Preuves mathématiques

Demaine-Demaine-Langerman-Langerman ont prouvé des bornes hautes 5D (141), 4T (192) et 4D (48) dans leur article "Morpion Solitaire". Pour le jeu 5T, ils ont prouvé une borne haute de 838 coups dans leur version 2004, améliorée à 704 coups dans leur version 2006. Toutefois deux petites erreurs dans leur article 2006 :



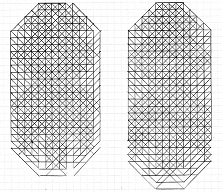
Mars 2003 : Grilles de 288 coups revendiquées être bornes hautes par Achim Flammenkamp
(image créée en oct. 2011 par Christian Boyer, cliquer pour agrandir)

    Auparavant, en mars 2003, Achim Flammenkamp (Université de Bielefeld, Allemagne) avait trouvé exactement la même borne haute de 705 coups et cette borne haute plus serrée de 288 coups, mais Demaine et al avaient été "unable to verify his proof sketch" (page 8 au-dessus). Voici cette preuve :

    Les grilles de 324 points décrites à la fin de sa preuve sont revendiquées être des bornes hautes. Toutefois, même si elles contiennent correctement 324 points, elles ne peuvent inclure les 324 - 36 = 288 lignes nécessaires comme vous pouvez le vérifier dans mon image de ses deux octagones limites : le premier avec b1 = 14, b2 = 26, d1 = d2 = 31 peut contenir un maximum de 264 lignes de cinq points, et le second avec b1 = 13, b2 = 28, d1 = d2 = 32 peut contenir un maximum de 270 lignes de cinq points.

    Plus bas, ma grille finale 5T de 317 coups contient correctement les 317 lignes nécessaires, et comme ce nombre est supérieur à ses 288 coups, cela prouve par l'exemple que son résultat n'est pas une borne haute : sa preuve de 288 coups est fausse, pourquoi s'auto-limiter aux formes octogonales ? Mais la preuve de 705 coups, trouvée à la fois par lui (= 741 - 36) et par Demaine et al (= 704 + 1), semble correcte.

    Novembre 2011, nouvelle version de Flammenkamp proposant, page 10, une borne haute 5T de 665 coups.

Dans les articles de Science & Vie, de nombreuses tentatives de bornes hautes 5T ont été données, mais sans preuve détaillée et/ou valide :

Il y a une autre borne haute 5T obtenue dans les années 70 :

En août 2010, Pekka Karjalainen, Oulu, Finlande, m'a envoyé une preuve de borne haute 5D de 138 coups, donc trois coups de moins que la borne haute de Demaine et coauteurs.

  Conférence par Yushi Uno sur sa nouvelle borne haute, à CCCG 2013

En juillet 2013, Akitoshi Kawamura (Université de Tokyo, Japon), Takuma Okamoto, Yuichi Tatsu, Yushi Uno, et Masahide Yamato (tous quatre de l'Université Osaka Prefecture, Japon) ont prouvé une nouvelle borne haute 5D de 121 coups. Cette preuve, initialement publiée dans arXiv, a été annoncée à CCCG 2013, la 25ème Canadian Conference on Computational Geometry qui s'est tenue en août 2013 à Waterloo, Ontario, Canada.

En janvier 2014, il ont publié dans arXiv une version 2 de leur article, ne changeant pas la borne haute de 121 coups, mais corrigeant une petite erreur (partie 4.2, nouveau lemme 2 remplaçant les anciens lemmes 2 & 3), et précisant que Peter Bartsch avait déjà trouvé une grille de 102 coups (figure 3, partie 4.3).

Grille record 5T++ (meilleure grille finale 5T connue) : 317 coups

Puisqu'à chaque coup de la partie on ajoute simultanément un point et une ligne, toute grille 5T (et aussi 5T+ et 5T#) de n coups a toujours, pendant le jeu ou à la fin du jeu :

Quel est le plus grand nombre possible de coups dans une grille finale respectant ces règles ? "Grille finale" signifie que l'on ne teste pas si il est possible ou impossible de réellement jouer cette grille coup par coup depuis la croix initiale.

Voici mon meilleur résultat, une grille 5T / 5T+ de 317 coups. Cela pourrait être la meilleure grille finale 5T et 5T+ possible, et par conséquence aussi une borne haute du score maximum, mais difficile à prouver... C'est en tout cas le record au jeu 5T++. Et c'est aussi un contre-exemple de la "preuve" de Flammenkamp de 288 coups.


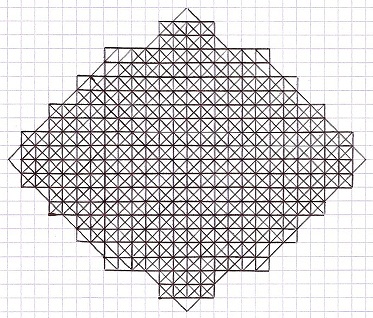
Novembre 2011 : Grille record 5T++, meilleure grille finale 5T connue, 317 coups, par Christian Boyer
 c.-à-d. 317 lignes (82 horizontales + 81 verticales + 77 diagonales/ + 77 diagonales\) , et 317 + 36 = 353 points

Le nombre de points initiaux a une grosse influence sur la meilleure grille finale possible. Avec seulement six points supplémentaires (36 + 6 = 42 points initiaux), on peut obtenir 535 coups, c'est-à-dire plus de deux cents coups supplémentaires ! Et avec encore douze points supplémentaires (42 + 12 = 54 points initiaux), on peut obtenir 829 coups ! Je pense que ces deux grilles sont les meilleures possibles pour ces nombres de points initiaux, mais à nouveau difficile à prouver. Dans ces trois grilles, l'astuce est la même : si vous regardez les quatre côtés comme des escaliers, chaque marche a une taille 2x2, sauf une marche plus large 4x2. Avec cette astuce, presque toutes les diagonales, mais aussi horizontales et verticales, sont des multiples de quatre segments, remplissant complètement l'intérieur sans laisser d'espace inutilisé.

   
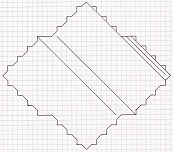
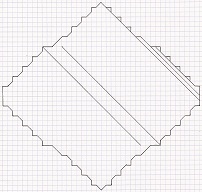
Novembre 2011 : Grille finale 5T de 535 coups avec 42 points initiaux, c.-à-d. 535 lignes et 577 points
 et grille finale de 829 coups avec 54 points initiaux, c.-à-d. 829 lignes et 883 points, par Christian Boyer.
Remplir les grilles est laissé comme exercice de patience au lecteur :-)

Comme vous pouvez le voir, mes grilles finales ressemblent à des losanges.
Contrairement à Flammenkamp qui n'utilise que des octogones.
Mais peut-être que quelqu'un construira de meilleures grilles finales, plus de coups avec les mêmes nombres de points initiaux ? Avec peut-être une forme encore différente ?

Scores minimum

Après les scores maximum, quid des scores minimum ? Je n'ai jamais vu aucune mention d'eux. Etrange... car il est très amusant de construire des mauvaises grilles ! Voici mes pires grilles possibles (d'autres exemples avec les mêmes nombres de coups sont possibles) :

       
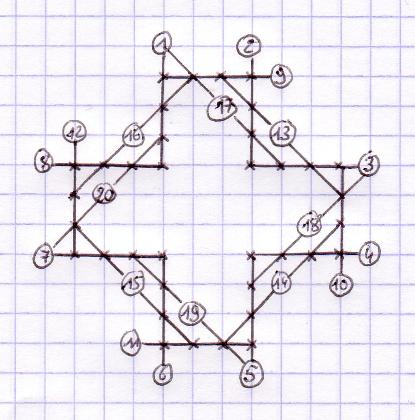
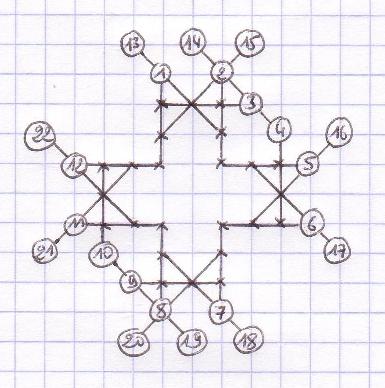
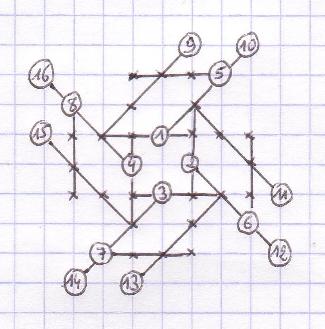
Janvier 2008 : exemples des plus mauvais jeux possibles au Morpion Solitaire, par Christian Boyer.
Respectivement jeu 5T/5D avec 20 coups, jeu 4T avec 22 coups, jeu 4D avec 16 coups.
(cliquer sur les images pour les agrandir)

Regardez les 22 coups du plus mauvais jeu 4T possible : il est étrangement impossible d'obtenir une grille aussi mauvaise qu'aux jeux 5T et 5D (20 coups).

Pendant son énumération, Michael Quist a confirmé en mars 2008 que mes scores sont bien les pires possibles, et a calculé le nombre des différentes grilles possibles :

© Christian Boyer, www.morpionsolitaire.com