
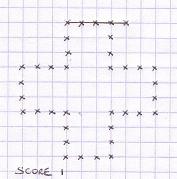
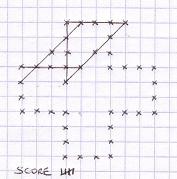
Initial pattern at 5T and 5D Morpion Solitaire, and example of a first move joining 5 crosses.
Morpion Solitaire - Rules of the Game
"Voici un passe-temps qui
risque de coûter plus cher aux bureaux et aux administrations que la grippe,
le téléphone et les cocottes réunis."
("Dilbert
would praise this pasttime as an efficient way of neutralizing an office worker
far beyond flu, phone, email and origami")
Pierre Berloquin, April
1974 (and his own free translation of May 2008)
Only one player is needed, and the rules are very simple. The equipment is also very simple: a paper (cross-ruled, if possible) and a pencil.
First draw the initial pattern below, looking as a large Greek cross. Then add a new small cross where you want, but only if 5 small crosses (including your new one) can be aligned. Draw the line across the 5 small crosses, and your score becomes 1.


Initial pattern at 5T and 5D
Morpion Solitaire, and example of
a first move joining 5 crosses.
Each time you add one small cross and draw its line (one and only one line), you add 1 to your score. A line can be horizontal, vertical, or diagonal. A line can cross or touch, but cannot overlap, a previously drawn line.
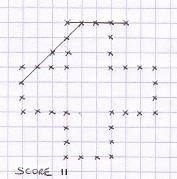
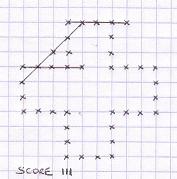
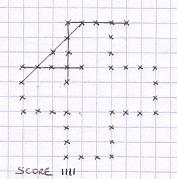
Examples
of next moves
The game ends when you become unable to
add a new cross (not caused by the paper, which is supposed to be unlimited in size).
The goal is to have the maximum score, and that's it! Very
easy, isn't it?
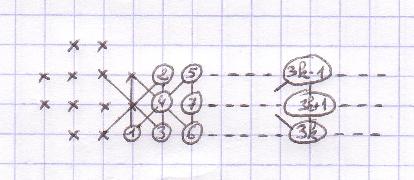
However, a remark. If you draw small crosses as above, it will later be difficult (*) to replay exactly the same game without knowing their order. If you reach 179 moves... better than the current record... it will be laborious to reconstruct your record. That's why it is recommended to number immediately each move, writing move numbers instead of crosses. The above game becomes:

It
is recommended to number the moves
(*) but possible, see "Verifying a drawing", part 4.1 of the Demaine et al paper
What are 5T, 5D, 4T, 4D games?
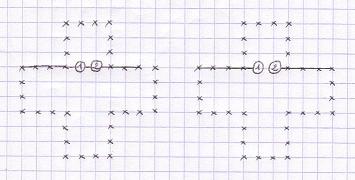
The move 2 on the left image
is possible in 5T game, but impossible in 5D.
The move 2 on the right image
is possible in both games.

Initial pattern at 4T and 4D
Morpion Solitaire
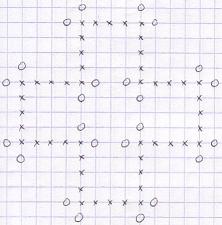
On
the left, an infinite score at 3T or 3D game. On the right, none of the possible
moves at 6T or 6D will generate any new possible move.
This figure on the left proves that the score of a 3T or 3D games CAN BE infinite. But as remarked in February 2008 by Lee Morgenstern, USA, it even seems that any game IS ALWAYS infinite. Who can prove that, or who can provide a counter example (a 3T or 3D game having a finite number of moves)? See also this variant: finite 3D/3T.
Michael Quist, USA, computed in March 2008 the number of different grids after n moves, n < 10. The number of grids grows very fast.
|
Move |
Number of different grids |
|
|
3D |
3T |
|
|
1 |
5 |
5 |
|
2 |
89 |
90 |
|
3 |
979 |
1004 |
|
4 |
9165 |
9699 |
|
5 |
71567 |
79234 |
|
6 |
497539 |
583619 |
|
7 |
3159820 |
3977770 |
|
8 |
18757312 |
25675388 |
|
9 |
105481614 |
159207030 |
© Christian Boyer, www.morpionsolitaire.com