Morpion Solitaire - Record Grids (5T game)

Rosin's grids of 177 and 178 moves: the new world records

Christopher D. Rosin (Milwaukee, Wisconsin, USA 1971 - ) in 2009 and 2010
(second photo by R. Brenson, Aurora, for Science & Vie, 2010)

August 12, 2011: new record with 178 moves! And again from Chris Rosin, one more move than his previous record announced only three months earlier, using an enhanced variation of the method described in his IJCAI paper. New record immediately announced by Pour La Science's website, also by Tangente N°143 of Nov-Dec 2011 (article p.44). Chris has lived in San Diego, California, since 1992, and is a cofounder of Parity Computing where he is Chief Algorithmist. His personal home page is www.chrisrosin.com

  
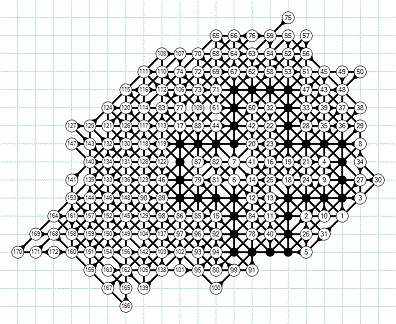
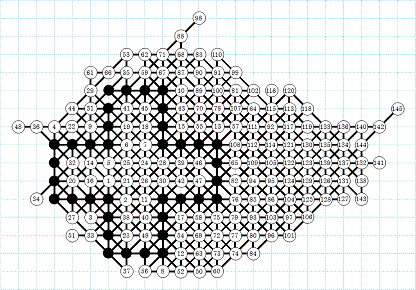
August 2011: Chris Rosin's grid of 178 moves
July 2011: Toby Walsh, Program Chair of IJCAI 2011, giving the award to Chris Rosin for his paper describing his record of 177 moves

May 19, 2011: date of his record of 177 moves, five more moves than his previous record of 2010. At this level, so many supplemental moves is a really extraordinary feat! Chris says he discovered his record January 16, but kept it secret because of his paper submitted to the IJCAI 2011, International Joint Conferences on Artificial Intelligence, Barcelona, Spain, July 2011. Using several microcomputers, he has done 28 runs of his C++ program, each run taking one week. Two runs on 28 gave two different grids of 177 moves. Sciences et Avenir announced this record in their July 2011 issue, page 23.

   
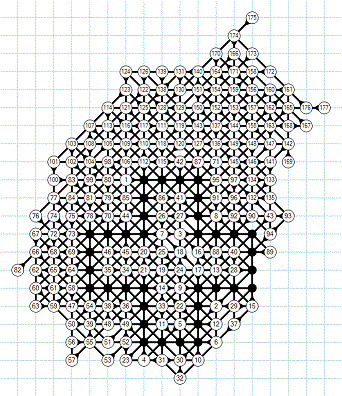
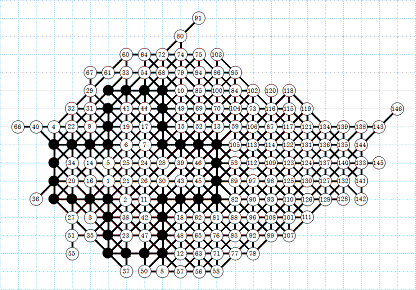
May 2011: Chris Rosin's grids A and B of 177 moves
When reoriented, these grids are close. See comparisons part.
(click on the images to enlarge them)

• Download the text file of the 178 moves or (A) of the 177 moves or (B) of the 177 moves, which you can use directly in Pentasol, a freely downloadable Windows software
• Download other grids of 178 moves, also in Pentasol format, and very close to Rosin's grid, at http://koozdra.wordpress.com/2013/12/21/a-collection-of-high-scoring-grids-in-pentasol-format/, where Dimitri Tishchenko, already author in 2011 of grids of 171 and 172 moves, compiled in December 2013 his best results from 157 to 178 moves.

Rosin's grid of 172 moves: the world record from 2010 to 2011

August 16, 2010: date of the previous record from Chris Rosin with 172 moves. With his grid obtained by computer, he is the first to have succeeded to beat the old record of 170 moves done 34 years earlier by C.-H. Bruneau without a computer! And this is tremendous progress with his new algorithm, the previous record obtained by computer having only 146 moves. Five days later, he also beats the 5D record.

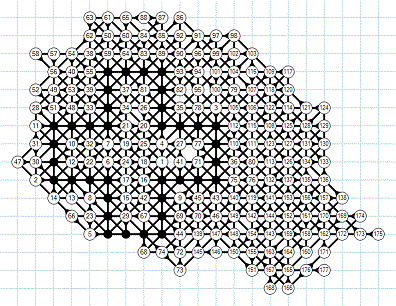
August 2010: Chris Rosin's grid of 172 moves

I notice that the road to his 172 moves is very tight: for the moves 132, 134, 135, 136, 144, 145, 150, 168, 170, 171 and 172, there is no other choice. It is the opposite of common sense: we may think that a record should offer several possible moves at each step. In Bruneau’s grid, only the last moves 169 and 170 were unique. Two files detailing Rosin's grid:

• See the animated GIF file (7.5Mb, created by C. Rosin) showing the game, move by move
• Download the text file of the 172 moves, which you can use directly in Pentasol, a freely downloadable Windows software

Here are some details on the search that Chris Rosin sent me:

Monte-Carlo search has had some recent success in the game of Go (for example: www.lri.fr/~teytaud/mogo.html), and also in other domains (including some of the recent Morpion Solitaire results by others). Monte-Carlo search methods operate by performing randomized "playouts" and then making moves which worked well in these playouts. In Morpion Solitaire, a "playout" consists of a randomized sequence of legal moves that proceeds until no further legal moves are available. An important factor for the success of Monte-Carlo search is the choice of playout policy, for biasing the randomized move choices during the playout. I spent several months developing and fine-tuning a playout policy for Morpion Solitaire, combined with some modified Monte-Carlo search techniques. This got me as far as 166 on the 5T game, but I could get no further. So I then threw out my fine-tuned playout policy, and tried instead to apply machine learning techniques to learn playout policies from scratch. This general idea has been tried in Go as well (D. Silver & G. Tesauro, "Monte-Carlo simulation balancing." ICML 2009). I combined this policy learning with nested search (somewhat like: T. Cazenave, "Nested Monte-Carlo Search." IJCAI 2009), and this succeeded in producing the result with 172 lines on August 16, 2010.

The code was written in C++. For the final version, I did 10 runs (each with a different random seed), with each run taking about 3 days on a single CPU core of a 3GHz Intel CPU. Two of these runs yielded 170 (not the same as Bruneau's grid), and one yielded the result with 172 lines.

I was very happy to publish a paper on his record in Science & Vie, the same French magazine in which Pierre Berloquin published the previous record by Bruneau... 34 years earlier! In my paper, testimonies of C. Rosin, C.-H. Bruneau, P. Berloquin. Thanks to them and also to Hervé Poirier, editor.

     
Science & Vie, November 2010: publication of Rosin's grid of 172 moves, by Christian Boyer
(click on the images to enlarge them, or download the PDF file, 856Kb)

And here are his two previous grids of 170 moves, equaling the score obtained in 1976 by C.-H. Bruneau (but different from Bruneau's grid):

The two first images are Rosin's grids A and B of 170 moves. I notice that these two grids are very close:
the third image C comes from the image B after rotation and symmetry, now looking like the image A.

• Download the text file (A) of the 170 moves, which you can use directly in Pentasol, a freely downloadable Windows software

Tishchenko's grids of 171 and 172 moves: equalling the world record of 2010

 Dimitri Tishchenko (Gomel, Belarus 1982 - ) in 2011, and one of his structures

April 11, 2011: Dimitri Tishchenko equals the world record of Chris Rosin with a different grid of 172 moves, before Rosin's new record of 177 moves announced one month later. And produces also a good grid of 171 moves. He uses what he calls a move's specific "DNA encoding". Look at his webpage http://koozdra.wordpress.com with http://koozdra.wordpress.com/2011/05/21/morpion-dna-encoding/

Dimitri Tishchenko lives in Victoria, British Columbia, Canada. He works for the Canadian Network for Public Health Intelligence (CNPHI) as a senior web application developer. He has a bachelors degree of computer science honors program from the University of Manitoba. He enjoys making geometric structures out of small neodymium magnetic spheres, and is fascinated by photography. See www.flickr.com/photos/38565795@N05/sets/ and www.trendhunter.com/trends/dimitri-tishchenko

   
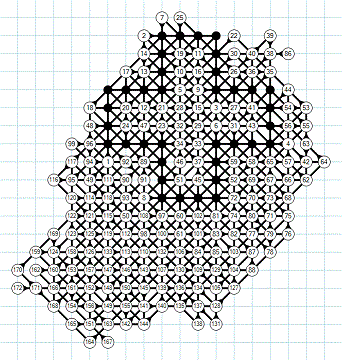
April 2011: Dimitri Tishchenko's grids of 171 and 172 moves
When reoriented, these grids are close. See comparisons part.

• Download the text file of the 171 moves, and of the 172 moves, which you can use directly in Pentasol, a freely downloadable Windows software

On his 172 grid, after move 80, we note that there is only one possible move 81! It is rare that the first imposed move comes so early, here move 81, so we may think that the game will soon finish. In the other good grids, the first imposed moves are 151 (Tishchenko 171), 157 (Rosin 177A), 146 (Rosin 177B), 169 (Bruneau 170), 132 (Rosin 172). Here are some details on his Morpion Solitaire search Dimitri sent me:

I originally heard of Morpion Solitaire from Reddit in May 2010. I was working on different algorithms and was able to generate a 158 at the end of July. I went on vacation to Europe and when I returned in mid August I saw that Chris Rosin had beaten the record. This meant my highest computed record became irrelevant. I continued to work on the problem refactoring my Morpion evaluation code and attempting different types of algorithms to get a higher record. I tried many different types of algorithms including genetic algorithms, simulated annealing, taboo search and Monte Carlo tree search. None were more effective than an algorithm that I created based on a "DNA" string that represents a Morpion configuration. Using this representation, modifications can be made to a configuration and still maintain unrelated structures. I developed other encodings but they were not very conducive to modification because future moves could be dependent on the modified move. The other parts of the algorithm are the modification strategy and peak avoidance. I spent quite a while fine-tuning the modification strategy and settled on something that, I believe, can be improved upon. Morpion Solitaire has very interesting peaks. I consider a peak to be a configuration where modifications only yield a small number of like scoring configurations. The internal structure of the configuration is solidified. Interestingly, these peaks do not only occur at high scoring configurations. Therefore the algorithm has to be able to recognize these peaks and back off to a lower scoring configuration where the internal structure is looser and more configurations can be generated.

I am still working on fine-tuning various parameters of the algorithm to try to beat the record...

Comparison of record grids

(This paragraph and its downladable files were written before Rosin's 178 grid, but all is still right. His new grid, here rotated 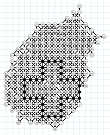, has again a lot of similarities compared to his previous 177A and 177B grids)

I note a lot of similarities, comparing the new grids of 2011. In order to better compare the record grids (including Bruneau), I have reoriented all of them, using rotations and symmetries, in the same way, increasing in the same direction.

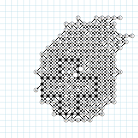
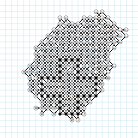
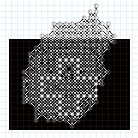
Bruneau 170,    Rosin 172,    Tishchenko 171,    Rosin 177B,    Tishchenko 172,    Rosin 177A

With the Powerpoint presentation (618Kb), or its equivalent PDF file (811Kb), showing clearly the similarities and differences, we can see that:

• Bruneau 170 is different from the others,
• Rosin 172 is different from the others,
• but Rosin 177A + Rosin 177B + Tishchenko 171 + Tishchenko 172 are of the same “family”, being similar during the beginning of the game, a large low part of the grids having the same shape. And Tishchenko 172 + Rosin 177A have a line (but not the same) going outside in their left part. At the end of the games, upper part of the four grids, they are different.

Tishchenko and Rosin did not collaborate, and their programs are different. Maybe it means that their methods are closer than we may think, and/or that their resulting grids are now close to "the" optimum grid?

Sending them this remark, here are their reactions, Dimitri:

When I originally sent the 171 and 172 grids I noticed the similarity between them. The two results were created on two independent computers running the same algorithm over a weekend. Both started with a completely random grid. I was actually very surprised that both had reached such a similar result. I think our techniques are similar. My DNA technique allows for alterations in the internal structure while maintaining a path to the current highest scoring grid. Alterations that create a significantly lower scoring grid are ignored. Chris's technique (as I understand it) is to find alternate paths in the internal structure that will lead to the current highest grid. His technique is much more methodical while my alterations are made at random.

And Chris:

Christian, your analysis is interesting. Each of the grids I have sent you is the result of an independent run of my software, and the runs start from a completely uniform random state with no seeding by any pre-existing shape. Dimitri's technique looks promising and there may be some similarity to what I'm using. My NRPA method maintains a distribution over solutions, and gradually updates that distribution to increase the chance of selecting elements that are part of the current highest grid. Dimitri's description "find alternate paths in the internal structure that will lead to the current highest grid" is roughly true with NRPA.

5T grids done by computer, before Rosin

Before Rosin's grid of 172 moves obtained in 2010, computers were unable to reach very big scores at this 5T game and to beat Bruneau's grid obtained by hand in 1976. The first big computed grids, 117 then 122 moves, were published by Hugues Juillé in his papers of 1995 then 1999, for his PhD thesis at Brandeis University, USA. Later, in January 2003, Pascal Zimmer reached 143 moves. Then in December 2007, Tristan Cazenave, LIASD, University of Paris 8, reached 144 moves:

December 2007: Grid of 144 moves done by computer by Tristan Cazenave

Haruhiko Akiyama (Tokyo, Japan 1987 - ) in 2010

The computing record became 145 moves, reached February 4th 2010 by Haruhiko Akiyama, a student of TUAT (Tokyo University of Agriculture and Technology). Using a modified "nested Monte-Carlo search" (see Cazenave's two papers of 2009), during 21 days he ran his own program written in C on a PC, Intel Core2Duo E8400 at 3.00GHz.

I notice, looking at the grid, that this record by computer can be improved by hand. For example (maybe among other possible improvements), it is easy to get 149 moves:

• move 23, instead of X-20-X-X-23, it would be better to play X-X-23-X-8, because then there is a new possible move with 48-146-X-20-X.
• move 18, instead of 5-6-18-X-10, it would be better to play 16-5-6-18-X (or X-16-5-6-18), because then there is a second new possible move with X-10-90-110-147.
• move 108, instead of 65-108-57-107-81, it would be better to play 82-65-108-57-107, because then there is a third new possible move with 107-81-99-148-147.
• renumber move 44 by a new move 32 (still obtained by 32-9-X-25-26), then instead of the old move 32 with X-32-20-X-27, play a new move 33 with 32(=old 44)-22-X-33-20, renumber old moves 33 to 43 by new moves 34 to 44, do not modify moves 45 to 148, and there is a fourth new possible move with 20-X-27-51-149.

Zbigniew Galias, Poland, has computed at the end of February 2010 that the last 71 moves of this grid improved at 149 moves are optimal.

February 16th 2010, Haruhiko Akiyama reached 146 moves: his program finally saw my last remark above and ended after 33 days of running. Renumbering the moves, my three other remarks can be again applied and allow to get 149 moves. With his professor Yoshiyuki Kotani, he published a paper in Japanese, reporting his grid of 145 moves (paper submitted before his new grid of 146 moves).

• Download the text file of the 145 moves, and of the 146 moves, which you can use directly in Pentasol, a freely downloadable Windows software

February 2010: Grids of 145 and 146 moves done by computer by Haruhiko Akiyama

Analyzing the symmetrical grids by computer, Michael Quist, USA, found this excellent and very nice grid of 136 moves, only 10 moves less than the above record! He thinks that it should be the best possible score of all symmetrical 5T grids (inversion symmetry like this one, but also diagonal reflection, horizontal reflection, 90-degree rotation, ...).

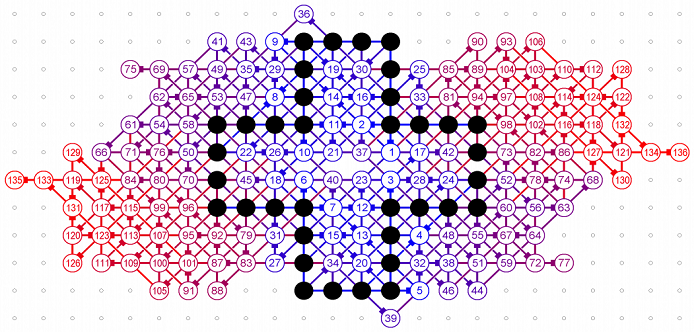
April 2008: symmetrical grid of 136 moves done by computer by Michael Quist

Jean-Jacques Sibilla, IPGP (Institut de Physique du Globe de Paris), http://www.ipgp.fr/~sibilla, is doing an interesting search: since 2007, his computer has generated two billion grids (status in October 2013), where the moves are done at random. His main results:

extremely difficult to get random grids of more than 100 moves, his best grid having 102 moves
two peaks at 21 and 64 moves
impossible to get fewer than 20 moves, as mentioned in the worst possible grids

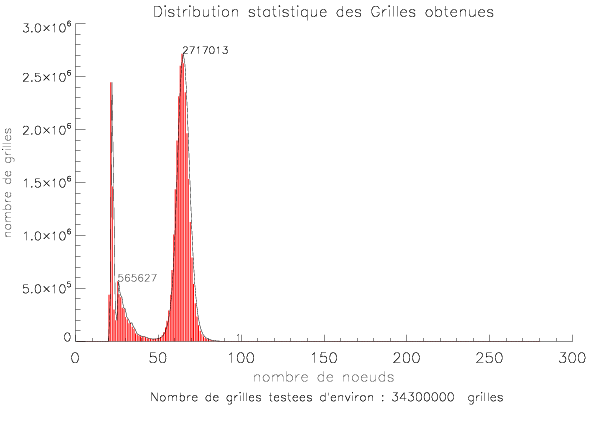
Scores after 34,300,000 random grids, computed by Jean-Jacques Sibilla

© Christian Boyer, www.morpionsolitaire.com