Morpion Solitaire - Variantes

Dans cette page :

Connector (deux joueurs)

Walter Joris par lui-même en 2002 (repris de son livre page 7)

Dans son livre "100 Strategic Games for Pen and Paper", Walter Joris a publié ce jeu pour deux appelé "Connector". Voici tel qu'il l'a publié, merci pour sa sympathique autorisation. Ce livre est aussi traduit et publié en espagnol, polonais et grec.

   
100 Strategic Games for Pen and Paper (Carlton Books, 2002). Pour les règles de "Connector", cliquer pour agrandir l'image de droite.

On peut penser qu'il y a une stratégie gagnante facile pour le deuxième joueur : toujours jouer le coup symétrique (par rapport au centre) du premier joueur. J'ai reçu cette remarque en mars 2008 de Vincent Everaert, l'auteur du jeu Morpiae détaillé dans la partie suivante de cette page. Michael Quist propose une règle additionnelle gardant le jeu intéressant : "laisser le premier joueur (seulement) placer un seul point additionnel à l'intérieur de la croix avant que le jeu démarre, ce qui casse la symétrie."

Mais le premier joueur peut lui-même casser cette symétrie, et donc la stratégie du deuxième joueur. Voici le début d'une partie envoyé en janvier 2014 par Maria Eichlseder, Institute for Applied Information Processing and Communications (IAIK), Graz University of Technology, Autriche, (http://www.iaik.tugraz.at/content/about_iaik/people/eichlseder_maria/). Si le coup du premier joueur est une ligne diagonale croisant le centre, alors bien sûr le second joueur ne peut plus jouer le coup symétrique par rapport au centre. Cela devrait être le SEUL cas : aucune ligne horizontale ou verticale ne peut bloquer le second joueur, aucune ligne diagonale ne croisant pas le centre ne peut bloquer le second joueur.


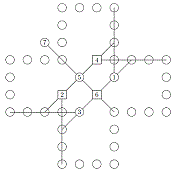
Contre-exemple de la stratégie gagnante du second joueur, par Maria Eichlseder, janvier 2014. Cliquer pour agrandir l'image.
Le second joueur ne peut jouer son coup 8 symétrique (par rapport au centre) au coup 7 du premier joueur.

Morpiae (deux joueurs)

Vincent Everaert, un inventeur français de plusieurs jeux (voir son site http://vincent.everaert.perso.sfr.fr), a publié en 2004 dans Tangente Jeux & Stratégie une autre variante du Morpion Solitaire pour deux joueurs. Il a aussi écrit un logiciel Windows gratuit jouant à ce jeu :

Les règles sont brièvement données en anglais dans la page Zillions of Games ci-dessus, et complètement décrites en français dans son article ci-dessous. Le jeu se termine quand plus aucun coup n'est possible, et le gagnant est celui qui a le maximum de points colorés.

     
Tangente Jeux & Stratégie n°11, nov.-déc. 2004. Pour les règles de "Morpiae", cliquer pour agrandir l'image de droite.

3D/3T fini (un joueur)

Puisque les parties 3D et 3T à partir du motif initial standard semblent toujours infinies, il est intéressant de chercher d'autres motifs initiaux permettant des parties 3D/3T finies.

A partir de ce motif initial utilisant une croix plus petite que le motif standard, même s'il est encore facile de générer des parties infinies, il est maintenant possible -mais très difficile- d'obtenir des scores finis au jeu 3D. Le plus petit score possible que j'ai pu trouver est de 23 coups. Est-il possible d'obtenir un plus petit score ?

En utilisant ce même motif initial, il semble impossible d'obtenir un score fini au jeu 3T. Ai-je raison, ou trouverez-vous une grille finie ?


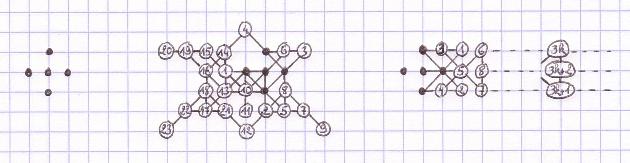
Avec ce motif initial au 3D/3T fini, facile d'obtenir des grilles infinies, mais difficile d'obtenir des grilles finies.
Mars 2008: grille 3D de 23 coups, par Christian Boyer.

En décembre 2011, Michael Quist a calculé les nombres des grilles distinctes possibles des 20 premiers coups au 3D fini, aucune de ces grilles n'est finie ! Cele signifie que le plus petit score N est :  21 ≤ N ≤ 23.

Nombre de grilles distinctes

Coup No

3D fini

1

2

2

11

3

41

4

182

5

870

6

4268

7

20348

8

93287

9

412591

10

1777469

11

7500990

12

31065049

13

126069994

14

500075924

15

1935406164

16

7302276390

17

26876695302

18

96680779037

19

340549953872

20

1176446002170

≥ 21

Unknown ≠ 0

Scaffold (un joueur)

Dans ses articles d'avrril 1976 et février 1977, Pierre Berloquin mentionnait un jeu proche du Morpion Solitaire nommé "Scaffold" (en français... "Echafaud" !), inventé par C. Croft, et publié en 1975 dans le magazine anglais Games and Puzzles. J'ai posé la question à Eric Solomon qui a un index complet de ce magazine à http://www.ericsolomon.co.uk/gpindex.html. Il m'a aimablement envoyé ce petit article (voir ci-dessous) tel que publié dans les pages de Puzzles préparées par David Wells. Pierre Berloquin mentionnait aussi une méthode de construction d'un scaffold de hauteur infinie trouvé par Harte et Brakes, mais Eric Solomon n'a pas trouvé cette réponse dans sa collection de Games and Puzzles. J'ai aussi posé la question à David Wells, il ne se rappelle pas de Harte et Brakes ni d'une réponse publiée au problème de Croft.

                           
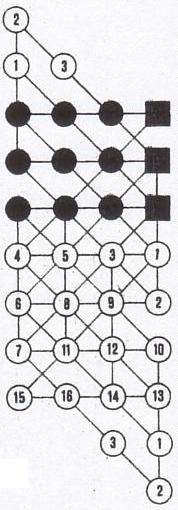
A gauche : problème de C. Croft publié par David Wells dans Games and Puzzles, n° 40, septembre 1975, page 36.
A droite : solution de Harte et Brakes d'une construction infinie publiée par Pierre Berloquin dans Science & Vie, février 1977, page 122.
(les trois carrés noirs sont les trois premiers coups directs à partir des neuf ronds noirs du motif initial)

5T dans un carré (un joueur)

Richard Cotté, professeur de mathématiques, jouait à une variante du jeu 5T quand il était un jeune étudiant en 1970. Le but était de remplir complètement le carré dans lequel la croix de départ est inscrite.

Cette variante n'est pas évidente... en voici une solution !


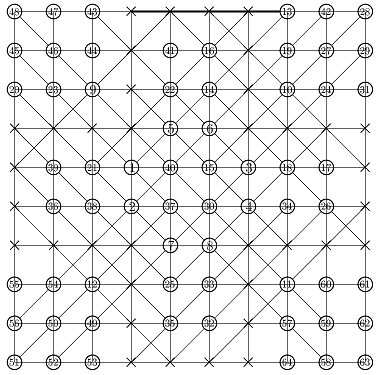
Une solution au 5T dans un carré, par Richard Cotté
(cliquer pour agrandir l'image)

Tsunami ! (un joueur)

Il est mathématiquement prouvé qu'un jeu 5T ne peut être infini avec un nombre fini de points initiaux, comme c'est le cas avec les 36 points de la croix initiale.

Mais est-il possible de complètement remplir le plan avec un motif initial donc infini, mais occupant partiellement le plan ?

Voici une solution trouvée par Michel Criton en 1976, et publiée par Pierre Berloquin dans Science & Vie, février 1977. Le motif initial occupe une petite bande (et seulement une) de quatre points de large, avec des rectanagles 4x4 répétés. En utilisant les règles 5T, après une première "vague" de points et lignes, la bande est plus large de un point chaque côté. Après une seconde "vague", la bande est plus large de deux points de chaque côté. Après une troisième "vague", la bande est plus large de trois points de chaque côté. Après une quatrième "vague", la bande est plus large de quatre points de chaque côté.

Puis, avec ces nouvelles bandes de quatre points que nous avons généré de chaque côté, on peut indéfiniment reproduire des séries similaires de quatre vagues : un tsunami, remplissant infiniment le plan !

               
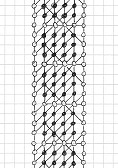
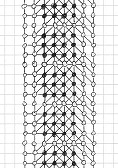
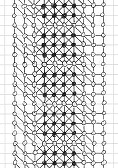
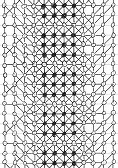
Motif initial, et la première série de 4 vagues du tsunami, par Michel Criton

Est-il possible de produire un tsunami avec une bande / motif moins dense ?

© Christian Boyer, www.morpionsolitaire.com